1. 特点：

对复杂的决策问题的本质、影响因素及其内容在关系等进行深入分析的基础上，利用较少的定量信息使决策的思维过程数学化，从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法。

2. 方法概述：

它的特征是合理地将定性与定量决策结合起来，按照思维、心理的规律把决策过程细致化（层次化、数量化）。运用层次分析法建模大体上可以分为以下四个步骤：

  • 建立递阶层次结构模型；
  • 构造出各层次中的所有判断矩阵；
  • 层次单排序及一致性检验；
  • 层次总排序及一致性检验。

2.1 递阶层次的建立

  1. 最高层：这一层次中只有一个元素，一般它是分析问题的预定目标和理想结果。
  2. 中间层：这一层次中包含为了实现目标所涉及的中间环节，主要是一些考虑指标和一些准则。
  3. 最底层：这一层次中包含为了实现目标可供选择的各种方案。
    层次分析法要解决的问题是，求出最底层对最高层的相对权重，以此对最底层的方案、措施进行排序，选择最优方案。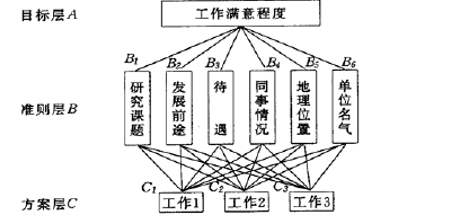

2.2 构造判断矩阵

  • 判别矩阵

$$ A = \begin{pmatrix}
a_{11}&…&a_{1n}\
\vdots &\ddots &\vdots \
a_{n1}&…&a_{nn}\
\end{pmatrix} = (a_{ij}){n*n}$$
在比较第 i 个元素与第 j 个元素相对于上一层某个因素的重要性时，使用数量化的相对重要度 $a{ij}$来表示。

  • 关于判别矩阵元素的确定:

2.3 层次单排序及一致性检验（一致性检验主要是为了避免矛盾）

  • 计算判断矩阵A的最大特征根$\lambda_{max}$和其对应的特征向量W$$AW = \lambda_{max}W$$
  • W和$\lambda_{max}$的求法一般采用方根法，和积发具体操作可以见文末视频。
  • 一致性检验是为了允许判断矩阵允许有不一致的范围
  • 一致性检验的步骤如下：
    1. 计算一致性指标CI：$$ CI =\frac{\lambda_{max} - n}{n - 1} $$CI = 0表示完全一致，CI越大越不一致
    2. 查询平均随机一致性指标RI，对应 n=1 到10。（具体RI值可以查找相关论文）
    3. 计算一致性比例CR：$$ CR = \frac{CI}{RI} $$当CR < 0.1时，认为矩阵的一致性是可以接受的。

2.4 层次总排序一致性检验

  • 即从上而下逐层进行各层元素对目标合成权重的计算

3. 学习文献